根与多项式系数关系
任何一个一元复系数多项式方程都至少有一个复数根。也就是说,复数域是代数封闭的 复数域代数封闭。
代数封闭:域$F$被称为代数闭域,当且仅当任何系数属于$F$且次数大于零的单变量多项式在$F$里至少有一个根。代数闭域一定是无限域。
不得不感慨,还是需要捡起一些遗忘的科目:),回忆下笔者和Galois理论的缘起。
对称多项式基本定理
对称多项式
对称多项式: 对于域$F$上的$n$元多项式$f(x_{1},x_{2},x_{3},\dots,x_{n})\in F[x_{1},x_{2},\dots,x_{n}]$,如果对于任意两个变量对换,原多项式保持不变,则这个多项式称为对称多项式。
等价定义:
$$ \forall σ \in \mathbb{S_n}, f(x_{σ(1)},x_{σ(2)},\dots,x_{σ(n)})=f(x_{1},x_{2},\dots,x_{n}) $$由此可以推出: 对于多项式 $f(x_{1},\dots,x_{n})$ 中的 $m$ 次项
$$ \prod_{k=0}^{m} x_{i_{k}}^{j_{k}} $$在置换后成为 $\prod_{k=0}^{m} x_{σ(i_{k})}^{j_{k}}$ 依然是 $f(x_{1},\dots,x_{n})$ 中的一项;故在所有置换下,得到所有项构成一个 $m$ 次齐次多项式:
$$ \sum_{σ \in \mathbb{Sn}} \prod_{k=0}^{m} x_{σ(i_{k})}^{j_{k}} $$任何一个单项式都可以置换产生一个齐次多项式。
例: 最简单的但现实每个变量次数不超过$1$:
$$ σ_{1} = \underset{1\le i \le n}{\sum} x_{i} = x_{1}+x_{2}+x_{3}+\dots+x_{n} $$例: 二次式$x_{1}x_{2}$经过置换可以得到二次齐次对称多项式:
$$σ_{2} = \underset{1\le i \le j \le n}{\sum}x_{i}x_{j} = x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{n}+x_{2}x_{3}+\dots+x_{n-1}x_{n} $$例: 三次情况:
$$ σ_{3}= \underset{1\le i \le j \le k \le n}{\sum } x_{i}x_{j}x_{k} $$一般的,对于k次多项式:
$$ σ_{k}= \underset{1\le i_{1} \le i_{2} \dots i_{n-1}\le i_{n} \le n}{\sum} x_{i_{1}}x_{i_{2}}\dots x_{i_{k}} $$基本对称多项式 特别地,对于$n$次式 $x_{1}x_{2}\dots x_{n}$ 本身就是一个$n$次齐次对称多项式$σ_{n}$。
推论
根据代数基本定理,在一个代数封闭域$F$上的$n$次首一多项式
$$ f'(x) = x^{n} + \sum_{i=1}^{n} a_{i}x^{n-i} $$都有$n$个零点,可分解为
$$f'(x)= \prod_{i=1}^{k}(x-x_{i}) $$展开后得到:
首一多项式的韦达定理
$$ f'(x)=x^{n}-σ_{1}x^{n-1}+σ_{2}x^{n-2}+\dots+(-1)^kσ_{k}x^{n-k}+(-1)^nσ_{n} $$对应相等得到根与系数关系:
$$ σ_{k} = (-1)^{k} a_{k}, 1\le k \le n $$一般的韦达定理
定义
$$ f(x) = \sum_{i=0}^{n} a_{i} x^{n-i} $$注意到上述特殊 $ f’(x) $ 为 $ F(x) $ 的 $ a_{0}=1 $ 的特殊情况, 所有系数均除以 $ f(x) $ 的 $ a_{0} $ ,现在重新定义域 $ F $ 上一般多项式的韦达定理。
一般的加入最高次项系数:
$$ \sigma_k^{\prime}=(-1)^k\frac{a_k}{a_0},1\leq k\leq n $$由此完成上述概念阐发的韦达定理内容。
基本多项式定理
对于任意域$F$上的多项式$f\in F(x_{1},x_{2},\dots,x_{n})$, 都存在多项式 $g \in F[x_{1},x_{2},\dots,x_{n}]$使得$f=g(σ_{1},σ_{2},\dots,σ_{n})$ 这一定理说明了基本多项式与原始多项式可相互表出。
基本对称多项式定理的证明
对于变量个数$n$进行归纳:
$n=1$时,结论成立。 假设$n-1$个变量时,结论成立,对于n个变量,结论也成立
$$σ_{k}= \sum_{1\le i_{1} \le \dots \le i_{k} \le n} x_{i_{1}x_{i_{2}}}\dots x_{i_{k}}$$$σ_{k}$为n元基本对称多项式。
$$\tau_{k}= \sum_{1\le i_{1} \le \dots \le i_{k} \le n} x_{i_{1}x_{i_{2}}}\dots x_{i_{k}}$$$\tau_{k}$为$n-1$元基本多项式。
对于
$$σ_{1}= \tau_{1}+x_{n},\tau_{1}=σ_{1}-x_{n}$$$$σ_{2} = \tau_{2} +\tau_{1}x_{n},\tau_{2}=σ_{2}-x_{n}σ_{1}+x_{n}^2$$
$$σ_{3}=\tau_{3}+\tau_{2}x_{n},\tau_{3}=σ_{3}-σ_{2}x_{n}+\tau_{1}x_{n}^2-x_{n}^3$$
$$\dots$$
$$σ_{n-1}=\tau_{n-1}+\tau_{n-2}x_{n}$$
$$σ_{n}=\tau_{n-1}x_{n},0=σ_{n}-σ_{n-1}x_{n}+\dots+(-1)^{n}σ_{1}x^{n-1}+(-1)^{n+1}x^n_{n}$$
所以对于是任意$n$元多项式$f\in F(x_{1},\dots,x_{n})$,可以写成
$$f= g_{n-1}x_{n}^{n-1}+\dots+g_{1}x_{1}+g_{0} = \sum_{i=0}^{n-1}g_{i}x^{i_{n}},g_{k}\in F(x_{1},x_{2},\dots,x_{n-1})$$注意到$f$为$n$元对称多项式,可得$f$在$x_{1},x_{2},\dots,x_{n-1}$的任意置换下不变。由此可得,$g_{k}$是$n-1$元对称多项式。
由归纳假设可得,$g_{k}$可由$\tau_{1},\tau_{2}\dots \tau_{n-1}$表出,即有:
$$ g_k=g_k(\tau_1,\tau_2,\cdots, \tau_{n-1}),~0\leq k\leq n. $$又$\tau_{k}$可用$σ_{1},σ_{2},\dots,σ_{n-1}$表出,代入:
$$f=f_{n-1}x_n^{n-1}+\cdots+f_1x_n+f_0$$其中 $f_k=f_k(σ_1,σ_2,\cdots,σ_n)$ 是 n 元对称多项式。
为了证明 $f$ 可以用 $σ_1,σ_2,\cdots, σ_n$ 多项式表示,只需要证明 $f_k=0,~1\leq k\leq n-1$ ,由此得到 $f=f_0$ .
把 $x_i$ 和 $x_n$ 对换得到
$f=f_{n-1}x_i^{n-1}+f_{n-2}x_i^{n-2}+\cdots+f_1x_i+f_0,~ 1\leq i\leq n.$
矩阵形式可表示为范德蒙矩阵系数形式:
$$ \begin{pmatrix} 1&x_1&x_1^2&\cdots& x_1^{n-1}\\\\ 1&x_2&x_2^2&\cdots& x_2^{n-1}\\\\ \vdots&\vdots&\vdots&\cdots&\vdots\\\\ 1&x_n&x_n^2&\cdots& x_n^{n-1} \end{pmatrix} \begin{pmatrix} f_0\\\\ f_1\\\\ \vdots\\\\ f_{n-1} \end{pmatrix}= \begin{pmatrix} f\\\\ f\\\\ \vdots\\\\ f \end{pmatrix} $$注意到解的唯一性,以及特解$f_{1}=f_{2}=\dots=f_{n-1}=0,f_{0}=f$为特解,可得$f=f_{0}$
经典表出
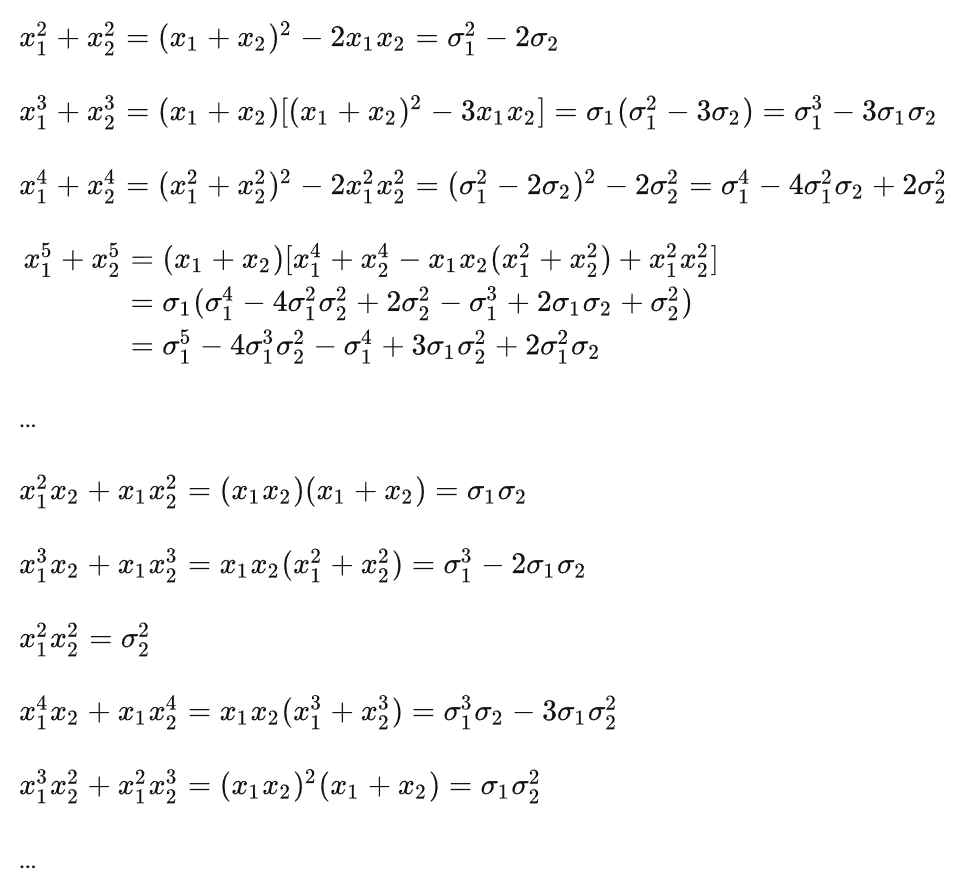
对于三次情况:
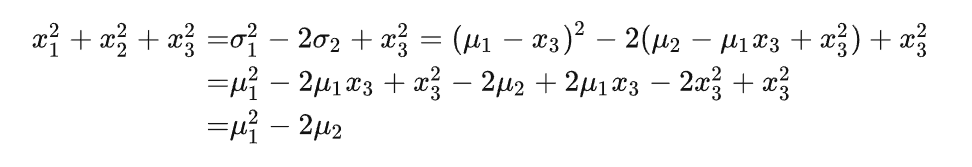
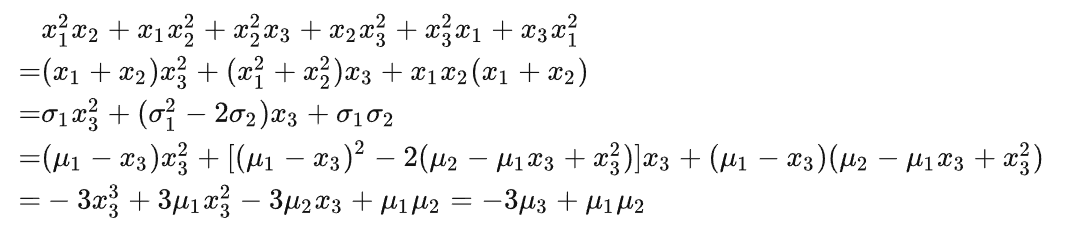
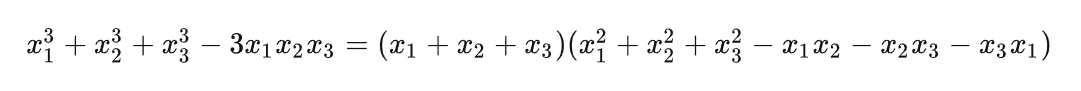
牛顿恒等式
特殊的对称多项式:
$$ S_{k} = σ_{i=1}^{n} x_{i}^{k} = x_{1}^k+x_{2}^k,+x_{3}^k+\dots+x_{n}^k,k=0,1,\dots $$牛顿恒等式
设 $x_1,x_2,\ldots,x_n$ 是 $a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0=0$ 的 n 个根,定义
根据韦达定理可知:
定义
$$p_{k}=x_{1}^{k}+\cdots+x_{n}^{k},k\in\{1,2,3\ldots\}$$有了对称多项式的概念和基本定理,不难理解牛顿恒等式的推导。 也注意到这里
$$\begin{aligned} e_{0} &=σ_{0} \\\\ e_{1} &=σ_{1} \\\\ e_{2} &= σ_{2} \\\\ & \vdots \\\\ e_{n} &=σ_{n} \\\\ e_{k} &=0, \quad \text { for } k>n \end{aligned}$$韦达定理可知:
$$e_{i} = (-1)^{n} \frac{a_{n-i}}{a_{n}}$$基本定理可得
$$p_k=\begin{cases}&e_1p_{k-1}-e_2p_{k-2}+\cdots+(-1)^{k-2}e_{k-1}p_1+(-1)^{k-1}ke_k &k\leq n \\\\ &e_1p_{k-1}-e_2p_{k-2}+\cdots+(-1)^{n-1}e_np_{k-n} &k>n\end{cases}$$利用递归计算$p_{k}$

高联科目一
Let $r_{1},r_{2},r_{3},r_{4},r_{5}$ be roots of $x^5+5x^4+10x^3+10x^2+6x+3$ Compute
$$ (r_{1}+5)^5+(r_{2}+5)^5+(r_{3}+5)^5+(r_{4}+5)^5+(r_{5}+5)^5 $$写出$f(x+5)$并化简,然后得到系数,代入恒等式即可。
不过可以有更多小Trick :)
$$f(x+5) = p_{5}+25p_{4}+250p_{3}+1250p_{2}+3125p_{1}+3125 \times 5$$$p_{i}$的计算过程:
$$\begin{aligned} p_1&=e_1p_0=-5 \\\\ p_2&=e_1p_1-2e_2=(-5)^2-2\cdot10=5 \\\\ p_3&=e_1p_2-e_2p_1+3e_3=(-5)\cdot5-10\cdot(-5)+3\cdot(-10)=-5 \\\\ p_4&=e_1p_3-e_2p_2+e_3p_1-4e_4=1 \\\\ p_5&=e_1p_4-e_2p_3+e_3p_2-e_4p_1+5e_5=10\\\\ \end{aligned}$$Trick: $x^5+5x^4+10x^3+10x^2+6x+3=(x+1)^5+(x+1)+1$ 令 $r_i=s_i+1,i\in{1,2,3,4,5}$ $\sum_{i=1}^5(s_i+5)^5=\sum_{i=1}^5(r_i+4)^5$ 其中, $r_i,i\in{1,2,3,4,5}$ 是方程 $x^5+x+1=0$ 的5个根. $e_1=e_2=e_3=0,e_4=1,e_5=-1$ $p_1=p_2=p_3=0,p_4=-4,p_5=-5$ $p_5+20p_4+0+0+0+4^5\cdot5=\boxed{5035}.\square$
科目二
对于多项式$f(x) = \sum_{i=0}^{n} a_{i}x^{n-i}$,已知条件如下,请将$a_{i}$写成以$a,b,c$标出的形式。
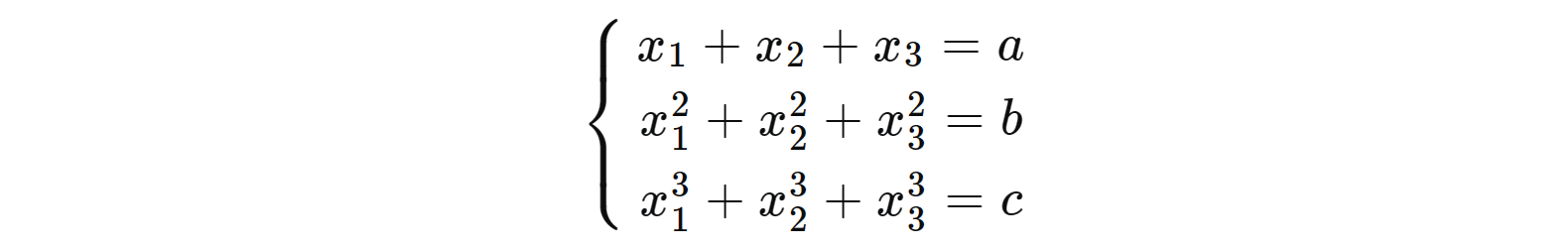
$$ \begin{aligned} &\sigma_{1} =x_1+x_2+x_3=a \\\\ &σ_2 =x_1x_2+x_2x_3+x_3x_1=\frac{a^2-b}2 \\\\ &σ_3 =x_1x_2x_3=\frac{\left(c+3a\frac{a^2-b}2-a^3\right)}3 \end{aligned} $$
根据上面得学习:
$$ σ_{k}= (-1)^{k}a_{k},1\le k \le n $$即
$$ \begin{aligned} &\sigma_{1} =x_1+x_2+x_3=a \\\\ &σ_2 =x_1x_2+x_2x_3+x_3x_1=\frac{a^2-b}2 \\\\ &σ_3 =x_1x_2x_3=\frac{\left(c+3a\frac{a^2-b}2-a^3\right)}3 \end{aligned} $$假设所求多项式$f(x)$的对应首一多项式为$f’(x)$,那么可得其对称多项式表出$g’(x)$
$$g'(x)= x^{3} - ax^{2} + \left( \frac{a^{2}-b}{2} \right)x - \frac{\left( c+ 3a \frac{a^{2}-b}{2}-a^3 \right)}{3}$$注意到定义多项式系数$a_{i}$定义在$\mathbb{Z}^+$上,故还原其中一个多项式为:
$$f(x)=-6x_{1}^2+6ax_{1}^2+(-3a^2+3b)x_{1}+a^3-3ab+2c$$一元三次方程求根公式
历史的进程
Scipione del Ferro 首先得出不含二次项的一元三次方程求根公式. Niccolò Fontana “Tartaglia” 独立得出一元三次方程求根公式. Girolamo Cardano 拜访了Tartaglia,并获得了包含一元三次方程求根公式的暗语般的藏头诗. Lodovico Ferrari Cardano的学生在一元三次方程的求根公式的基础之上,给出了一元四次方程的求根公式 Galois 证明了,如果一个五次方程的置换群是一个不可分离的群,那么这个方程就没有求根公式
Cardano法
对于 一般的一元三次方程
$$ f(x) = ax^{3}+bx^{2} +cx +d=0,a,b,c,d\in C,a \ne 0\tag{1} $$由代数基本定理,在复数域上有三个根。
简化为一元三次首一多项式:
$$f'(x) = x^{3}+ b'x^{2}+ c'x +d' \tag{2}$$配方法代换:
令$z= x+ \frac{b’}{3}$(消去二次项为目的)
$$z^{3} + pz + q = 0 \tag{3}$$令$z= u+v$
$$ (u+v)^{3}+p(u+v)+q=0 $$整理得:
$$ u^{3}+ v^{3} +3uv(u+v)+p(u+v)+q=0 $$即:
$$(u+v)(3uv+p)=-q-(u^3+v^3)\tag{4}$$考虑一种特殊的情况
$$\begin{cases}3uv +p &= 0 \\\\ u^{3}+v^{3}+q &= 0 \end{cases}\tag{5}$$显然方程组$(5)$一定有解,且$(5)$的解一定是不定方程$(4)$的一个解。退而求其次,先找到原方程的一个解先。
$$(u^{3} - v^{3})= (u^3+v^3)^2-4u^3v^3$$代入得
$$(u^3-v^3)^2=q^2+\frac{4}{27}p^3$$不妨取:
$$\begin{aligned} u^{3}&= - \frac{q}{2} \pm \sqrt{ \frac{q^2}{4}+\frac{p^3}{27} }\\\\ v^{3}&= - \frac{q}{2} \mp \sqrt{ \frac{q^2}{4}+\frac{p^3}{27} } \end{aligned} $$特殊化
$$\begin{cases} u^3 &= - \frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}} \\\\ v^3 &= - \frac{q}{2}- \sqrt{\frac{q^2}{4}+\frac{p^3}{27}}\end{cases}$$不难开三次方,在得到$z=u+v$就是一元三次方程的一个根。
判别式$\Delta= \frac{q^2}{4}+\frac{p^3}{27}$即为判别式。
考虑特殊情况: $x^{3}=1$的三个根。
欧拉公式
$$e^{i\theta} = \cos \theta + i \sin \theta$$
注意到,$\omega^{3} =1,\omega = e^{\frac{2\pi i}{3}}=\frac{-1+\sqrt{ 3 }i}{2}$
不难得到
$$\begin{cases}\omega&=e^{\frac{2\pi i}3}=\frac{-1+\sqrt{3}i}2\\\\ \omega^2&=e^{\frac{4\pi i}3}=\frac{-1-\sqrt{3}i}2\\\\ \omega^3&=e^{2\pi i}=1&\end{cases}$$恰好构成一个三阶循环群,可以在复平面内表示这三个根。
回到方程$z^{3}+pz +q = 0$:
$u=u_{0},v= v_{0}$是方程组$(5)$的一个解, 那么,由工具$\omega$可得方程组$(5)$的三组不同解:
$$\begin{cases}z&=\omega^0u_0+\omega^0v_0\\\\z&=\omega^1u_1+\omega^1v_1\\\\z&=\omega^2u_2+\omega^2v_2\end{cases}$$至此,我们的求解已经完成.
代回的形式可表示为:
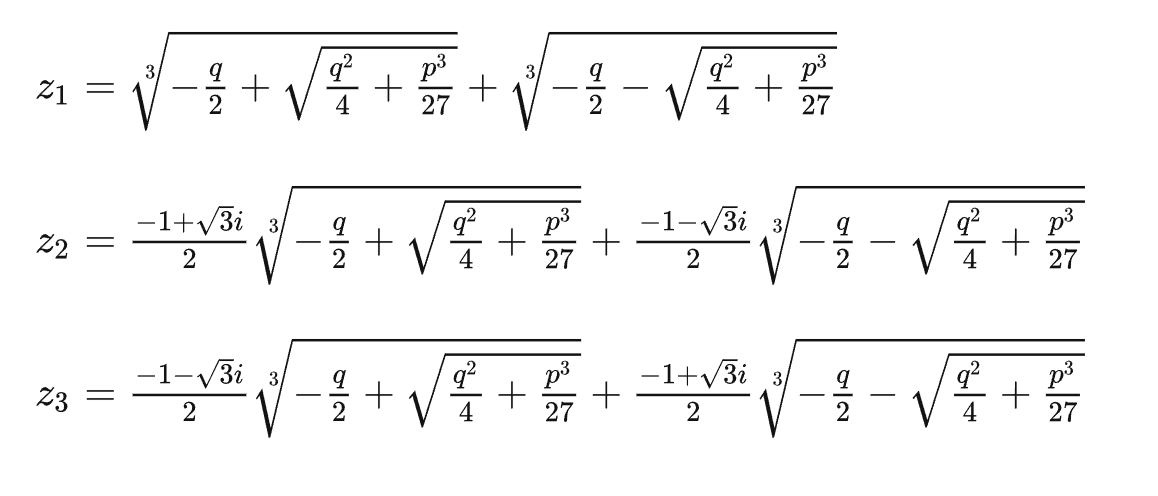
判别式$\Delta= \frac{q^2}{4}+\frac{p^3}{27}$即为判别式
- $\Delta > 0$,方程有1个解
- $\Delta = 0$,方程有2个解
- $\Delta < 0$,方程有3个解
判别式的一般定义:
对于多项式$P(x)=a_{n}x_{n}+a_{n-1}x_{n-1}+\dots+a_{1}x+a_{0}$,在复数域上存在$n$个根 $x_{1},x_{2},\dots,x_{n}$其判别式为
$$\Delta=a_{n}^{2n-2}\Pi_{1 \le i \le j \le n}(x_{i}-x_{j})^2$$显然$\Delta$为一个对称多项式.
例: 二次情况。
$$\Delta=(x_{1}-x_{2})^2=(x_{1}+x_{2})^2-4x_{1}x_{2}=b^2-4ac$$这更直接的告诉我们:根之间的关系,是否相等,这才是判别式的本质,解一元多次方程的关键,这触及了群论的本质——对称。
Crypto实践
|
|
|
|