Lattice Part 1
Regev讲义学习笔记
Everything Before
我们的目标是求解近似求解SVP问题,基于此构建了一个具有特殊结构的基,为了构建这样的代数结构,设计出一类规约算法,并验证了正确性和时间复杂度的可行性。基于这样的思路,可以在规约算法上进行优化,在代数结构上进行调整,获得更好的近似求解表现。
在具有这样的清晰思路后,再来考虑代数工具的构建,将会使工作更加完善。
Reduced Basis
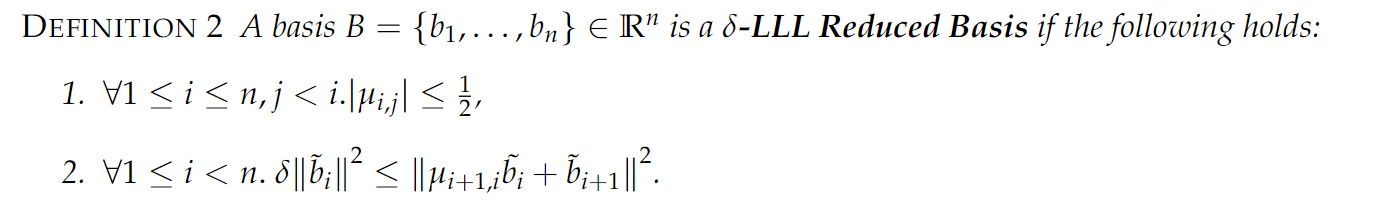
注意到 将一个普通正交基,规约为一个约简基总是可以的。
给出这样的定义,实则是基于我们的研究对象一些代数上表现良好的结构,使得可以很好的利用这样的约简基,配合闵可夫斯基界,我们可以给出一个SVP的近似求解,对于近似精度,我们再利用参数 $\delta$ 来进行很好的刻画,在后面的学习中将会看到这里的 $\delta = \frac{3}{4}$ 时,会得到一个非常良好的规约结果。
利用简单的三角不等式:
$$ \begin{cases} \delta{\Vert\tilde{b_{i}}\Vert}^{2}\leq{\Vert\mu_{i+1,i}\tilde{b_{i}}+\tilde{b_{i+1}}\Vert}^{2}=\mu_{i+1,i}^{2}{\Vert\tilde{b_{i}}\Vert}^{2}+{\Vert\tilde{b_{i+1}}\Vert}^{2} \tag{1} \\\\ \Vert\tilde{b_{i+1}}\Vert^2\geq(\delta-\mu_{i+1,i}^2)\Vert\tilde{b_i}\Vert^2\geq(\delta-\frac{1}{4})\Vert\tilde{b_i}\Vert^2 \end{cases} $$实际上,我们的格工作在 $p$ 范数空间。
进一步的,$(1)$,说明了两个相邻基向量不会相差太大
Schmit process中,不难发现, 所得到的基向量列向量优先可以得到,如下矩阵
即 从
$$ \tilde{b_i}=b_i-\sum_{j=1}^{i-1}\mu_{i,j}\tilde{b_j},where\mu_{i,j}=\frac{\langle b_i,\tilde{b_j}\rangle}{\langle\tilde{b_j},\tilde{b_j}\rangle}. $$到如下矩阵的一个转变
$$ \begin{pmatrix}\Vert\tilde{b_1}\Vert& \* &\cdots& \* \\\\ 0&\Vert\tilde{b_2}\Vert&\cdots& \* \\\\ \vdots&&\ddots&\vdots \\\\ &&& \* \\\\ 0&\cdots&&\Vert\tilde{b_n}\Vert\end{pmatrix} $$当 $\delta = \frac{3}{4}$ 时,所得矩阵概览便为:
$$ \begin{pmatrix}\Vert\tilde{b_1}\Vert&\leq\frac12\Vert\tilde{b_1}\Vert&\cdots&&\leq\frac12\Vert\tilde{b_1}\Vert \\\\ 0&\Vert\tilde{b_2}\Vert&\cdots&&\leq\frac12\Vert\tilde{b_2}\Vert \\\\ \vdots&&\ddots&&\vdots \\\\ &&&&\leq\frac12\Vert\tilde{b_{n-1}}\Vert \\\\ 0&\cdots&&&\Vert\tilde{b_n}\Vert\end{pmatrix} $$以上的工作均是在 Gram-Schmit 做微调下,实现这样的结果,但是直到现在我们尚未把所做工作同 SVP-approximation 联系起来。
What can LLL do?

更清晰的来说:

Short Vector and Reduced basis
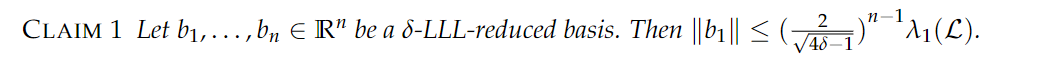
接下来我们证明CLAIM 1.
为了用符号语言的形势推导,我们引入 $\lambda_i$, 也是格中最为基础的参数之一。

针对这一定义可推导出
$\lambda_1(\mathcal{L}(B))\geq\min_{i=1,…,n}\Vert\tilde{b}_i\Vert>0.$
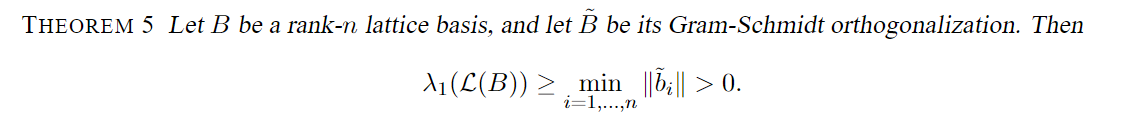
施密特正交化处理所得正交基向量的范数一定小于等于第一最短向量。
同样的,直觉的感受需要同形式化的证明相结合,利用求和符号、范数、正交的一些性质可得到
PROOF: Let $x\in\mathbb{Z^n}$ be an arbitrary nonzero integer vector, and let us show that $\Vert Bx \Vert \geq \min{\Vert\tilde{b_i}\Vert}.$ Let $j\in{1,\ldots,n}$ be the largest such that $x_j \neq 0.$
Then
$$ |\langle Bx,\tilde{b_j}\rangle|=|\langle\sum_{i=1}^jx_ib_i,\tilde{b_j}\rangle|=|x_j|\langle\tilde{b_j},\tilde{b_j}\rangle=|x_j|\Vert\tilde{b_j}\Vert^2 $$where we used that for all $i<j,\langle b_i,\tilde{b_j}\rangle=0$ and that $\langle b_j,\tilde{b_j}\rangle=\langle\tilde{b_j},\tilde{b_j}\rangle.$ On the other hand, $\Vert \langle Bx,\tilde{b_j}\rangle \Vert \leq \Vert Bx \Vert \cdot \Vert\tilde{b_j}\Vert$, (Cauchy-Schwarz Inequality) ,and hence we conclude that
$$ \Vert Bx \Vert \geq \|x_j\| \Vert\tilde{b_j}\Vert\geq\Vert\tilde{b_j}\Vert\geq \min{\Vert\tilde{b_i}\Vert.} $$这里需要指明的是 $Bx$ 可视为 $x$ 经线性变换 $B$, 得到在变换后空间中的表示。
即可以可逆矩阵 $B$ 作为线性变换,可以视为一种映射。
进一步的
PROOF The Claim
回顾刚刚的CLAIM1:
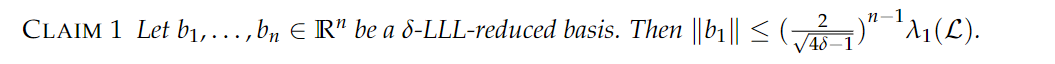
至此,应用 $\lambda$ 的性质,以及施密特正交基的最短 ( $l_2$ 意义上) 基向量与 $\lambda_1(\mathcal{L})$ 的关系,利用简单的系数放缩,便可以完成证明,也同时很好的将我们最开始定义 Reduced Basis 的工作同 SVP 问题相结合。
PROOF: Since for any basis $b_1,\ldots,b_n,\lambda_1(\mathcal{L})\geq\min_i\Vert\tilde{b_i}\Vert$,we get that
$$ \Vert\tilde{b_n}\Vert^{2} \geq(\delta-\frac{1}{4})\Vert\tilde{b_{n-1}}\Vert^{2} \geq \ldots \geq(\delta-\frac14)^{n-1} \Vert\tilde{b_1}\Vert^{2} =(\delta-\frac{1}{4})^{n-1}\Vert b_{1} \Vert^2 $$where the last equality follows by the definition $\tilde{b_1}=b_1.$ Then, for any $i$,
$$ \Vert\tilde{b_1}\Vert\leq\left(\delta-\frac14\right)^{-(i-1)/2}\Vert\tilde{b_i}\Vert\leq\left(\delta-\frac14\right)^{-(n-1)/2}\Vert\tilde{b_i}\Vert. $$Hence,
$$ \Vert b_{1} \Vert \leq \left(\delta-\frac{1}{4}\right)^{-(n-1)/2} \min_i{\Vert\tilde{b_i}\Vert} \leq \left(\delta-\frac{1}{4}\right)^{-(n-1)/2} \cdot \lambda_{1}(\mathcal{L}) $$对于 $\delta = \frac{3}{4}$ 的情况,代入即可:
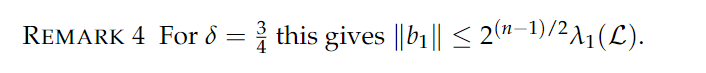
此时,我们已经说明了一个代数结构,很好的符合了我们 SVP-Approximation 的出发点,于此我们引入算法上的工作,这包含了算法设计与时间复杂度分析。时间分析这部分暂略过,值得注意的是 LLL 的表现好于保守分析的结果。
Way to LLL
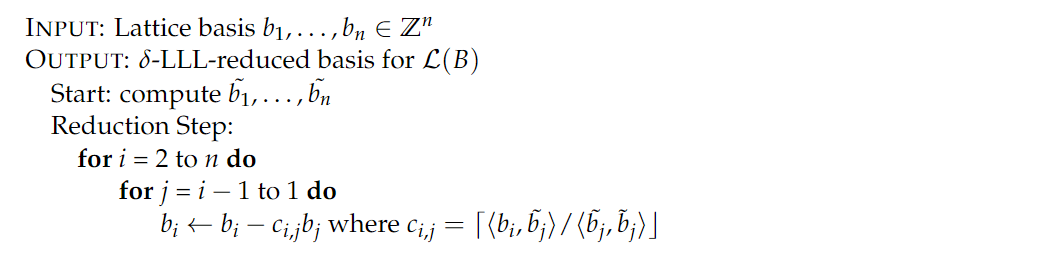

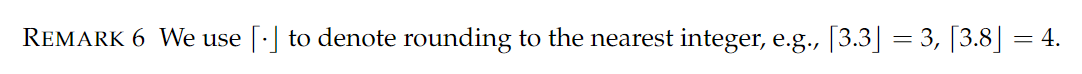
也即我们现在要完成一个矩阵到矩阵的变换。
初等列变换保证矩阵的可逆性,加入线性乘子保障范数符合条件。在施密特正交化过程中加入 REMARK 6 ,保证了这里的系数 $\frac{1}{2}$ , 而 SWAP 过程保证 约简基性质2.
严格意义上的

Open Probelm

Application

我们将继续深入探究格规约所带来的全新分析视角。