Lattice Part 3

Begin with Knapsack.

Note from CS355 & Regev.

Short Integer Solution (SIS) problem

Definition

The SIS problem is parameterized by the matrix dimensions $n,m \in \mathbb{N}$, modulus $q$, and a norm bound $B$ on the solution.

• One should think of $n$ as the parameter $\lambda$ that defines the hardness of the problem. The bigger $n$ is, the harder the problem becomes.
• The parameter $m$ is set depending on the specific applications, but generally $m \gg n$.
• The modulus $q$ can be set to be any $q = \operatorname{poly}(n)$, but concretely, just think of $q = O(n^2)$.
• The norm bound $B \ll q$ should also be set depending on the specific applications.

Notice that a solution $z$ for $A$ can be converted to a solution for the extension $[A|A^{\prime}]$ by appending $0$s to $z$:

• big $m\Rightarrow$ easy (the more vectors we are given, the easier the problem becomes)
• big $n\Rightarrow$ hard (the more dimension we work in the harder the problem becomes)

It is conjectured that for any sufficiently large $n \in \mathbb{N}$ (this is the security parameter), for any $m,q,B \in \mathbb{N}$, satisfying $q \gt B\cdot\operatorname{poly}(n)$ (for any polynomial poly) , the $\text{SIS}(n,m,q,B)$ is hard.

But we cannot say that Short Integer Solution (SIS𝑆𝐼𝑆) problem is NP-Complete.

Application: CRHF, SLHL etc.

SIS 问题可以最终规约到格中的 SIVP 问题上，进而在选定参数的情况下，在部分情况下是可以求解的。一般的，Inhomogeneous SIS （非齐次情况）在 CTF 中遇到的更多.

Without Modulus

Modification

Let $n$ be an integer and $\alpha=\alpha(n),\beta=\beta(n),m=m(n)>\Omega(n\log\alpha)$ be functions of $n$.Sample a uniform $A\leftarrow[-\alpha,\alpha]^{n\times m}$.The task is to compute “short” vector $e\in\mathbb{Z}^m$ in the kernel of $A$. That is: $$ \begin{cases} \Vert e \Vert &\lt \beta \\ A \cdot e &= 0^n \end{cases} $$ Here, equality holds over the integers.

Trivial attack: There is an trivial algorithm in the case where $\beta$ is huge. You can compute a kernel vector over the integers by taking minors of the matrix $A$.These minors, and hence the kernel vector, can be easily upper bounded by $(\alpha n)^{O(n)}$. So in the regime $\beta=(\alpha n)^{O(n)}$, there is a trivial attack.

It’s intersting to care about the distribution on matrix $A$.

However it is still no doubt that if limiation of norm is set, then the problem is set to be hard.

Inhomogeneous Short Integer Solution (ISIS) problem

Inhomogeneous SIS is applied for OWF (one way function) and then Digital Signatures. We shall mentioned it in subsequent notes.

Inhomogeneous linear equations

即对于这样的线性方程，可以考虑它的解空间，对于这样的解空间可以找到他的一组正交基，由于我们工作在整数上，即纯量域为 $\mathbb{Z}$ ，所以所得基向量，可张成 Lattice .

自然地，考虑非齐次线性方程

$$ \langle a,z\rangle\equiv c\mathrm{~mod~}q\tag{5.2} $$

首先，注意到 $\vec{0}$ 不是 Eq. 5.2 的一个解，那么 Eq. 5.2 的解便无法构成一个格空间。

特别的，$\mathcal{x} \in \mathbb{Z}^{n}$ 是 Eq. 5.2 一个解，当且仅当 $\mathcal{x} - \mathcal{z}$ 是方程的一个解。那么代数上来看 Eq. 5.2 的所有解可以表示为齐次方程的解空间的一个陪集：

$$ \mathcal{L}+z $$

这里，我们需要将找到 Eq. 5.2 一个 $l_2$ 范数意义上较短的解，同 CVP 联系起来。如过只是找到一组解，而没有任何范数意义上的限定，这样的求解是十分trivial的。

Solving linear equations for short integer solution.

当我们在用格规约一组方程所在线性空间的基向量时，我们在做什么？

Gaussian expected shortest length

Definition. Let $\mathcal{L}$ be a lattice of dimension $n$. The $\textit{Gaussian expected shortest length}$ is

$$ \sigma (L)=\sqrt{\frac{n}{2\pi e}}(\det L)^{1/n} $$

The Gaussian heuristic says that a shortest nonzero vector in a“ randomly chosen lattice" will satisfy $$ \Vert v_\text{shortest}\Vert \approx\sigma(\mathcal{L}) $$

More precisely, if $\epsilon\gt 0$ is fixed, then for all sufficiently large $n$, a randomly chosen lattice of dimension $n$ will satisfy

$$ (1-\epsilon)\sigma(\mathcal{L})\leq\Vert v_{\mathrm{shortest}}\Vert \leq(1+\epsilon)\sigma(\mathcal{L}) $$

注意到，$\Vert v_{\mathrm{shortest}} \Vert = \lambda_1(\mathcal{L})$

容易联想到，此前 Minkowski’s Second Theorem 给出的行列式为单的上界

$$ \left(\prod_{i=1}^n\lambda_i\right)^{1/n}\leq\sqrt{n}(\det\Lambda)^{1/n} $$

然而这仅仅给出 $\lambda_i$ 的增长速度是受到行列式限制的，或者说，$\lambda_i$ 的排布相对紧 (tight). 但这里 Gaussian 从概率的角度给出了 $\lambda_i$ 的期望值，并引入 $\epsilon$ 给出了一个关于 $\lambda_i$ 的一个更紧的界。

Recall LLL property LINK

Let $B = \set{b_1,…,b_n}$ be a $\delta$-$LLL$-reduced basis.

Then $$ \Vert b_1 \Vert \le \left(\frac{2}{\sqrt{4\delta-1}}\right)^{n-1}\lambda_{1} \le\left(\frac{2}{\sqrt{4\delta-1}}\right)^{n-1}\sqrt{n}\cdot\Vert\det(\mathcal{L})\Vert^{1/n} $$ 利用这一中间界：

Conclusion

$$ \begin{cases} \Vert B\Vert \le \sigma(\mathcal{L}),\mathcal{L}\text{~is~}\mathcal{L}(B) \\ v\mathcal{L} = w\end{cases} $$ 即我们令 $\Vert B\Vert = \det \mathcal{L} \le \sigma(\mathcal{L})$, 此时只需判定这个不等式是否成立来判定 LLL 的解的情况。

至此我们只需要把目标问题化归到 $\gamma$-SVP 即可。

那么一般思路就是，构造合适的 lattice , 将我们的目标短向量嵌入其中，调整行列式大小 (re-scale the lattice) 来进行规约以求解。这里有时用到了 Embedding Technique .

Embedding Technique

前文有提到，非齐次状态下的小范数求解，可证明为 CVP 问题，也可化归到工作在陪集 $\mathcal{L} - t$ 上的 SVP 问题，现介绍一种手法来近似求解这一问题。

令基向量矩阵为$B$，给定目标向量 $t = c$，那么一般的构造如下矩阵：

$$ B^{\prime} = \begin{bmatrix} c & B \\ 1 & 0 \end{bmatrix} $$

注意到

$$ \det B^{\prime} = \det B $$

那么

$$ \operatorname{vol}B^{\prime} = \operatorname{vol} B $$

令目标向量 所得 CVP 的解为 $x = \sum \lambda_i b_i$ . 那么此时在 $B^{\prime}$ 中存在短向量 $(c-x,1)$ (Embedding) . 此时完成了一个近似CVP的解。

那么一定条件下，只需将待求非齐次方程 $ u = \sum a_i x_i$转化为 目标向量 求解即可。值得注意的是，有时需要先调整行列式大小，再规约，然后再做相反的调整。

更详细的证明，会在接下来的Knapsack 中给出解释。

Knapsack Cryptography

相比于RSA的模幂运算，背包密码的运行速度要快的多。

在非齐次情况下求解小范数根，了解 Knapsack Cryptography 及其 attack 是十分有帮助的。

The Subset-Sum Problem

We begin by recalling the definition of the subset-sum problem, also called the “knapsack” problem, in its search form.

Superincreasing sequence

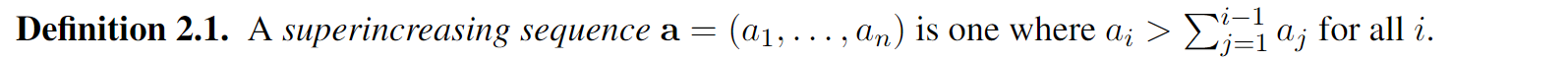
Merkle Hellman

Start with some superincreasing sequence $\boldsymbol{b} = (b_1,\dots,b_n)$ Choose some modulus $m>\sum_{i=1}^n b_i$, uniformly random $w \leftarrow\mathbb{Z_m}^{*}$ and uniformly random permutation $\pi$ on $\set{1,\dots,n}$ Let $a_i=w\cdot b_{\pi(i)}\mod m$.

The public key is $a = ( a_1, \ldots , a_n)$, and the trapdoor is $(m,w,\pi).$

The encryption of a message $\mathbf{x}\in{0,1}^n$ is then

$$ s=\mathsf{Enc_\mathbf{a}}(\mathbf{x})=\langle \vec a,\mathbf{x}\rangle=w \cdot \sum_{i=1}^{n} b_{\pi(i)} x_{i}. $$

Given the trapdoor $(m,w,\pi)$, we can decrypt $s$ as follows:

Simply compute

$$ s^{'}=w^{-1}s=\sum_{i=1}^{n} b_{\pi(i)}x_i\mod m $$

then solve the subset-sum problem for the permuted superincreasing $b$ and $s^{\prime}$.

上述描述的原始 Knapsack 过程直接规约在 CVP 即可求解。在实际过程中不必考虑置换过程，直接考虑原始置换后的向量为目标向量即可。

Density

The density of a subset-sum problem instance is $$ n/\max_i \log a_i $$

Lagarias-Odlyzko, Frieze

同样的利用上面给出的思路证明这个引理，但需要加入一些概率视角。

证明的核心思路为Embedding Technique.

PROOF

在构造完 $\bold{B}$ 后，$(x,0)^T \in B$. 最后一行系数 $B$ 用于放缩.

值得关心的是这个算法取得目标向量的概率。 $$ \bold{Bz}= (x,0)^T \in \mathcal{L},\Vert \bold{Bz}\Vert \le \sqrt{n} $$ 对于这个格空间内的任一向量，最后一项为 $B$ 的倍数时（不含0），那么 $$ B \gt 2^{n/2}\cdot \Vert x \Vert \ge 2^{n/2}\cdot \lambda_1(\mathcal{L}) $$ 故而 $\bold{B}$ 的 LLL 规约结果一定会有末项为 $0$ 的向量, 且范数最大为$2^{n/2}\sqrt n$。( LLL property ) 故而在密度（density）不合适的时候，这里可能会解出 $k(x,0)$.

在处理格的概率分析时，只需要严格抓住格的均匀分布特征即可。不难有如下描述

引入参数 $\epsilon$ 来刻画 $O(1)$

Summary

Knapsack

这里重新给出一个简单版本的表述：

私钥为一个超递增序列 $\set{a_n}$ , 满足 $a_i\gt \sum_{k=1}^{i-1}a_k$ , 模数$m$ ,满足$m>\sum_{i=1}^na_i$ ,乘数$w$ ,满足 $\gcd ( w, m) = 1$ . 公钥为$\boldsymbol{b} = (b_1,\dots,b_n)$ ,满足 $b_i\equiv wa_i\pmod m$ 加密：设明文为 ${v_i},v_i\in{0,1}$ ,则密文 $c$ 可表示为：

$$ c \equiv \sum_{i=1}^{n} b_i v_i \equiv \sum_{i=1}^{n} wa_i v_i \pmod m $$

明文$v$:

$$ v = w^{-1}c \equiv \sum_{i=1}^{n} v_i a_i \pmod m $$

构造矩阵

$$ \mathcal{L} = \begin{bmatrix} I & \boldsymbol{b}^T \\ 0 & -c \end{bmatrix} $$

$v = (v_1, \dots, v_n, 0) \in \mathcal{L}$. 利用高斯启发式，可以证明我们能够规约出$v$.

$$ \sigma(\mathcal{L}) = \sqrt{\frac{n}{2\pi e}}\Vert det\mathcal{L} \Vert^{1/(n+1)} = \sqrt{\frac{n}{2\pi e}} c^{1/(n+1)} $$

而

$$ \Vert v \Vert \approx \sqrt{n/2} \le \sigma(\mathcal{L}) $$

即

$$ \frac{1}{\pi e} c^{2/(n+1)} \le 1 $$

有$1-2^{-n^2(\varepsilon-o(1))}$有解。

References

• Babai’s Algorithm
• Knapsack
• Shortest Lattice Vectors in the Presence of Gaps
• Tover’s Blog
• ISIS problem discussion in LINK1,LINK2
• SIS problem discussion in LINK1
• A decade of lattice cryptography
• Cryptohack gitbook
• ISIS-small-q-code ISIS-small-q-paper
• Embedding attack