By which to Rule Them All

上回书说到 UOV …

基础

有限域 (Finite Field)

向量空间

双线性形式（Bilinear Form）

设域为有限域 $\mathbb{F}_q$，考虑向量空间 $\mathbb{F}_q^n$。双线性形式是一个函数：

$$ B : \mathbb{F}_q^n \times \mathbb{F}_q^n \to \mathbb{F}_q $$

满足以下两个条件：

1. 对每个固定的 $y \in \mathbb{F}_q^n$，映射 $x \mapsto B(x, y)$ 是 $\mathbb{F}_q$-线性的；
2. 对每个固定的 $x \in \mathbb{F}_q^n$，映射 $y \mapsto B(x, y)$ 也是 $\mathbb{F}_q$-线性的。

也就是说，$B$ 关于两个变量都是线性的。

对称双线性形式与二次型的关联

对称双线性形式（Symmetric Bilinear Form）

一个映射 $f: \mathbb{K}^n \times \mathbb{K}^n \to \mathbb{K}$ 满足：

• 双线性性：
  

  $$ f(a\mathbf{u} + b\mathbf{v}, \mathbf{w}) = a f(\mathbf{u}, \mathbf{w}) + b f(\mathbf{v}, \mathbf{w}) $$

  （对第一个变量的线性性）

• 对称性：
  

  $$ f(\mathbf{u}, \mathbf{v}) = f(\mathbf{v}, \mathbf{u}) $$

  传导后可得，对于两个变量均为线性。

“关联"的本质

二次型 $Q$ 和对称双线性形式 $f$ 通过 极化恒等式（Polarization Identity）联系：

$$ \boxed{f(\mathbf{u}, \mathbf{v}) = \frac{1}{2} \left[ Q(\mathbf{u} + \mathbf{v}) - Q(\mathbf{u}) - Q(\mathbf{v}) \right]} $$

反之，二次型 $Q$ 可由 $f$ 直接导出：

$$ Q(\mathbf{u}) = f(\mathbf{u}, \mathbf{u}) $$

关键关系总结

方向	公式	含义
$Q \to f$	$f(\mathbf{u},\mathbf{v}) = \frac{1}{2}[Q(\mathbf{u}+\mathbf{v}) - Q(\mathbf{u}) - Q(\mathbf{v})]$	从二次型恢复双线性形式
$f \to Q$	$Q(\mathbf{u}) = f(\mathbf{u},\mathbf{u})$	从双线性形式定义二次型

---

二次型与其极化形式（Polarization）

给定一个二次型（Quadratic Form）：

$$ f : \mathbb{F}_q^n \to \mathbb{F}_q $$

我们定义其极化形式（polar form）或称为极形式 $f^*$ 为：

$$ f^\*(x, y) = f(x + y) - f(x) - f(y) $$

这个形式具有以下性质：

• $f^*(x, y)$ 是一个双线性形式；

• 若 $f$ 是正规二次型（即 $f(ax) = a^2 f(x)$），则 $f^*$ 是对称的双线性形式，即：

  $$ f^{\*}(x, y) = f^{\*}(y, x) $$

举例（矩阵表示）

设 $f(x) = x^\top M x$，其中 $M$ 是一个 $n \times n$ 的矩阵，定义在 $\mathbb{F}_q$ 上，则：

$$ \begin{aligned} f^*(x, y) &= f(x + y) - f(x) - f(y) \\\\ &= (x + y)^\top M (x + y) - x^\top M x - y^\top M y \\\\ &= x^\top M y + y^\top M x \end{aligned} $$

如果 $M$ 是对称的（即 $M^\top = M$），则有：

$$ f^*(x, y) = 2 x^\top M y $$

注意：在特征为 2 的域中（即 $q$ 为 2 的幂），$2 \equiv 0$，所以：

$$ f^*(x, y) = x^\top M y + y^\top M x = 0 \quad \text{（如果 $M$ 是对称的）} $$

这使得在奇特性域（特征为 2）中，二次型与其极形式的关系非常特殊，常常导致极形式退化。

子空间

子空间是 $F_q^n$中闭合于加法和标量乘法的子集。关键类型包括：

• 各向同性子空间：存在非零向量 x 使 f(x)=0。
• 全各向同性子空间：所有向量 x 满足 f(x)=0，如UOV中的油子空间 O。
• 各向异性子空间：非零向量 x 满足 f(x)≠0。

全各向同性子空间的维数上限为 $⌊n/2⌋$，对UOV的安全性分析至关重要。

矩阵核

秩

矩阵的秩是其最大线性无关行或列数。二次形式的秩为其关联矩阵的秩，在奇特性场中保持不变。

一般线性群 $GL_n(F_q)$

由 Fq 上所有可逆 n×n 矩阵组成的群，出现在VOX方案的变换矩阵中。

One Vector to rule them all

Lemma 1

略.

Lemma 2

说明了 所谓迷向子空间 (Isotropic Subspace) ，即视为一组基向量矩阵的子空间表达，有其 rank 的特征 $r \gt n// 2$.

📜引理陈述

设 $f$ 是定义在域 $\mathbb{K}$ 上的秩为 $n$ 的二次型，$\mathcal{O}$ 是其任意全迷向子空间，则：

$$ \dim(\mathcal{O}) \leq \left\lfloor \frac{n}{2} \right\rfloor $$

关键概念回顾

1. 二次型与对称双线性形式

• 二次型：函数 $Q: \mathbb{K}^n \to \mathbb{K}$，可表示为 $Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x}$（$A$ 对称矩阵）

• 关联的对称双线性形式 $f$：

  $$ f(\mathbf{u}, \mathbf{v}) = \frac{1}{2} \left[ Q(\mathbf{u} + \mathbf{v}) - Q(\mathbf{u}) - Q(\mathbf{v}) \right] $$

  满足：

  • 双线性性：$f(a\mathbf{u}+b\mathbf{v},\mathbf{w}) = af(\mathbf{u},\mathbf{w}) + bf(\mathbf{v},\mathbf{w})$
  • 对称性：$f(\mathbf{u},\mathbf{v}) = f(\mathbf{v},\mathbf{u})$
  • 关系：$Q(\mathbf{u}) = f(\mathbf{u}, \mathbf{u})$

2. 全迷向子空间

子空间 $\mathcal{O} \subseteq \mathbb{K}^n$ 满足：

$$ \forall \mathbf{u}, \mathbf{v} \in \mathcal{O}, \quad f(\mathbf{u}, \mathbf{v}) = 0 $$

3. 矩阵表示

在基 ${\mathbf{v_1},\dots,\mathbf{v_n}}$ 下，$f$ 的矩阵为：

$$ A_{n \times n} = (a_{ij}) , \quad a_{ij} = f(\mathbf{v_i}, \mathbf{v_j}) $$

证明步骤（反证法）

步骤 1：反证假设

假设 $\dim(\mathcal{O}) = r > \left\lfloor \frac{n}{2} \right\rfloor$，则：

• 当 $n$ 偶：$r > \frac{n}{2}$
• 当 $n$ 奇：$r > \frac{n-1}{2}$

步骤 2：基扩充

取 $\mathcal{O}$ 的基 $B = {\mathbf{v_1},\dots,\mathbf{v_r}}$，扩充为 $\mathbb{K}^n$ 的基：

$$ \hat{B} = \{\mathbf{v_1},\dots,\mathbf{v_r}, \mathbf{v_{r+1}},\dots,\mathbf{v_n}\} $$

步骤 3：构造零块矩阵

在基 $\hat{B}$ 下，$f$ 的矩阵表示为：

$$ A = \begin{pmatrix} \boxed{\text{0}} & {\*} \\\\ {\*} & {\*} \end{pmatrix} $$

其中左上角的 $r \times r$ 子矩阵为：

$$ \begin{pmatrix} f(\mathbf{v_1},\mathbf{v_1}) & \cdots & f(\mathbf{v_1},\mathbf{v_r}) \\\\ \vdots & \ddots & \vdots \\\\ f(\mathbf{v_r},\mathbf{v_1}) & \cdots & f(\mathbf{v_r},\mathbf{v_r}) \end{pmatrix} = \begin{pmatrix} 0 & \cdots & 0 \\\\ \vdots & \ddots & \vdots \\\\ 0 & \cdots & 0 \end{pmatrix} $$

零块形成原因：

$$ \forall i,j \leq r,\ \mathbf{v}_i,\mathbf{v}_j \in \mathcal{O} \implies f(\mathbf{v}_i,\mathbf{v}_j) = 0 $$

步骤 4：秩分析

矩阵 $A$ 的结构：

$$ A = \begin{pmatrix} 0_{r \times r} & B_{r \times (n-r)} \\ C_{(n-r) \times r} & D_{(n-r) \times (n-r)} \end{pmatrix} $$

1. 前 $r$ 行：形如 $(0,\dots,0, b_{1,r+1},\dots,b_{1n})$
   张成空间维数 $\leq n - r$

2. 后 $n-r$ 行：无特殊约束
   张成空间维数 $\leq n - r$

3. 总秩上界：

   $$ \operatorname{rank}(A) \leq \underbrace{(n - r)} + {\underbrace{(n - r)}} = 2(n - r) $$

步骤 5：导出矛盾

由假设 $r > \left\lfloor \frac{n}{2} \right\rfloor$ 可得：

$$ r > \frac{n}{2} \implies n - r < \frac{n}{2} \implies 2(n - r) < n $$

因此：

$$ \operatorname{rank}(A) \leq 2(n - r) < n $$

但 $f$ 的秩为 $n$，要求 $\operatorname{rank}(A) = n$，矛盾！

结论

假设不成立，故必有：

$$ \dim(\mathcal{O}) \leq \left\lfloor \frac{n}{2} \right\rfloor \quad \blacksquare $$

几何解释

全迷向子空间维数上界 $\left\lfloor \frac{n}{2} \right\rfloor$ 反映了：

1. 在欧几里得空间中（正定二次型），全迷向子空间只能是 ${0}$
2. 在闵可夫斯基空间中（符号差 $(n-1,1)$），最大全迷向子空间维数为 $1$
3. 在辛空间中（交错形式），存在维数为 $n/2$ 的全迷向子空间

Notations in Cryptanalysis

Forgery - from one msg to a space

Key Recovery - as the name said.

Forgery

Forgery In RSA

from $e$ and leakage derive the set $S$

$$ S = \set{d_i | a^{ed_i} \equiv a \pmod n, \forall a \quad in \quad \mathbb{Z_n}} $$

UOV Scheme

Para

UOV（Unbalanced Oil and Vinegar）签名方案由以下参数确定：

• $m$：二次方程的个数（也是输出维度）
• $n$：变量个数（输入维度），通常 $n > m$
• $q$：有限域的大小（通常是小的素数或 $2$ 的幂）

设工作在有限域 $\mathbb{F}_q$ 上。

公钥与私钥结构

• 公钥：由 $m$ 个二次型构成的函数向量：

  $$ G = (G_1, \dots, G_m), \quad G_i : \mathbb{F}_q^n \to \mathbb{F}_q $$

  每个 $G_i$ 是一个二次齐次多项式。

• 私钥：由一组特殊结构的映射组成：

  • 一个多变量二次映射 $F : \mathbb{F}_q^n \to \mathbb{F}_q^m$，其中：

    $$ F(\mathbf{x}) = (F_1(\mathbf{x}), \dots, F_m(\mathbf{x})) $$

    每个 $F_i$ 是构造得使前 $m$ 个变量（称为 oil）在其中只以线性形式出现；

  • 一个可逆的线性变换矩阵 $A \in \mathrm{GL}_n(\mathbb{F}_q)$，用于隐藏结构。

私钥使得：

• 存在一组向量 $\mathbf{o}_1, \dots, \mathbf{o}_m \in \mathbb{F}_q^n$，使得其张成空间 $\mathcal{O} = \mathrm{span}(\mathbf{o}_1, \dots, \mathbf{o}_m)$ 是每个 $G_i$ 的二次齐次部分的 迷向子空间（totally isotropic subspace）；

• 即对于所有 $\mathbf{u}, \mathbf{v} \in \mathcal{O}$，有：

  $$ G_i^{(2)}(\mathbf{u} + \mathbf{v}) - G_i^{(2)}(\mathbf{u}) - G_i^{(2)}(\mathbf{v}) = 0 $$

签名过程（Signer）

给定私钥 $(A, F)$，签名者希望对消息 $\mu \in {0,1}^*$ 生成签名。

1. 计算哈希值：

   $$ \mathbf{z} = \mathcal{H}(\mu) \in \mathbb{F}_q^m $$

2. 多次尝试以下过程直到成功：

   • 随机选取 Vinegar 变量 $\mathbf{v} \in \mathbb{F}_q^{n - m}$

   • 将其代入 $F(\mathbf{x})$，只剩 $m$ 个未知量（oil 变量），求解线性方程组：

     $$ F(\mathbf{o}, \mathbf{v}) = \mathbf{z} $$

   • 若有解，拼接得 $\mathbf{x} = (\mathbf{o}, \mathbf{v})$

3. 应用线性变换：

   $$ \mathbf{y} = A^{-1} \mathbf{x} $$

4. 输出签名：

   $$ \sigma = \mathbf{y} $$

验签过程（Verifier）

验证者已知公钥 $G$，以及消息 $\mu$ 和签名 $\sigma = \mathbf{y}$。

1. 计算哈希值：

   $$ \mathbf{z} = \mathcal{H}(\mu) $$

2. 验证：

   $$ G(\mathbf{y}) \stackrel{?}{=} \mathbf{z} $$

Oil & Vinegar 变量

在私钥构造中，我们将变量分为两类：

• Oil（油）变量：前 $m$ 个变量 $x_1, \dots, x_m$
• Vinegar（醋）变量：剩余的 $v = n - m$ 个变量

私钥映射 $F$ 被构造得使得每个 $F_i$ 对 oil 变量是线性的，因此在给定 vinegar 值后，求解 $F(\mathbf{x}) = \mathcal{H}(\mu)$ 成为一个线性问题。

Kipnis-Shamir Attack

From this attack, the authors observed some facts.

lemma3

Key Observation

lemma4

Lemma 4 证明解析

给定条件

• $G = (G_1,\ldots,G_m)$ 是秩为 $n$ 的齐次二次映射，由 $m$ 个矩阵表示

• $\mathcal{O}$ 是 $G_1,\ldots,G_m$ 的公共全迷向子空间

• 取非零向量 $\boldsymbol{x} \in \mathcal{O} \setminus {\mathbf{0}}$

• 定义：

  $$ J(\boldsymbol{x}) = \left( \boldsymbol{x}^{T} G_{1}, \ldots, \boldsymbol{x}^{T} G_{m} \right) $$

  （雅克比矩阵去掉常系数）

需证明

1. $\mathcal{O} \subset \ker(J(\boldsymbol{x}))$
2. $\ker(J(\boldsymbol{x}))$ 一般是 $(n-m)$ 维子空间

---

证明步骤解析

步骤 1：证明 $\mathcal{O} \subset \ker(J(\boldsymbol{x}))$

1. 应用全迷向性质
   由 Lemma 1，对任意 $\boldsymbol{z} \in \mathcal{O}$ 和任意 $G_i$：

   $$ g_i(\boldsymbol{x}) = g_i(\boldsymbol{z}) = 0 \quad \text{且} \quad g_i^{\*}(\boldsymbol{z},\boldsymbol{x}) = 0 $$

   其中 $g_i^*$ 是与 $G_i$ 关联的双线性形式。

2. 构造线性形式
   固定 $\boldsymbol{x}$ 后，定义线性形式：

   $$ g_{\boldsymbol{x}}^i(\cdot) = g_i^\*(\boldsymbol{x},\ \cdot\ ) $$

   全迷向性质表明：

   $$ g_{\boldsymbol{x}}^i(\boldsymbol{z}) = g_i^*(\boldsymbol{x},\boldsymbol{z}) = 0 $$

   故 $\mathcal{O} \subset \ker(g_{\boldsymbol{x}}^i)$。

3. 矩阵形式等价
   线性形式 $g_{\boldsymbol{x}}^i$ 可表示为：

   $$ g_{\boldsymbol{x}}^i(\boldsymbol{v}) = \boldsymbol{x}^T G_i \boldsymbol{v} $$

   因此有：

   $$ \ker(g_{\boldsymbol{x}}^i) = \ker(\boldsymbol{x}^T G_i) $$

4. 建立包含关系
   由上述得：

   $$ \mathcal{O} \subset \bigcap_{i=1}^m \ker(\boldsymbol{x}^T G_i) $$

   而根据定义：

   $$ \ker(J(\boldsymbol{x})) = \bigcap_{i=1}^m \ker(\boldsymbol{x}^T G_i) $$

   故证得：

   $$ \mathcal{O} \subset \ker(J(\boldsymbol{x})) $$

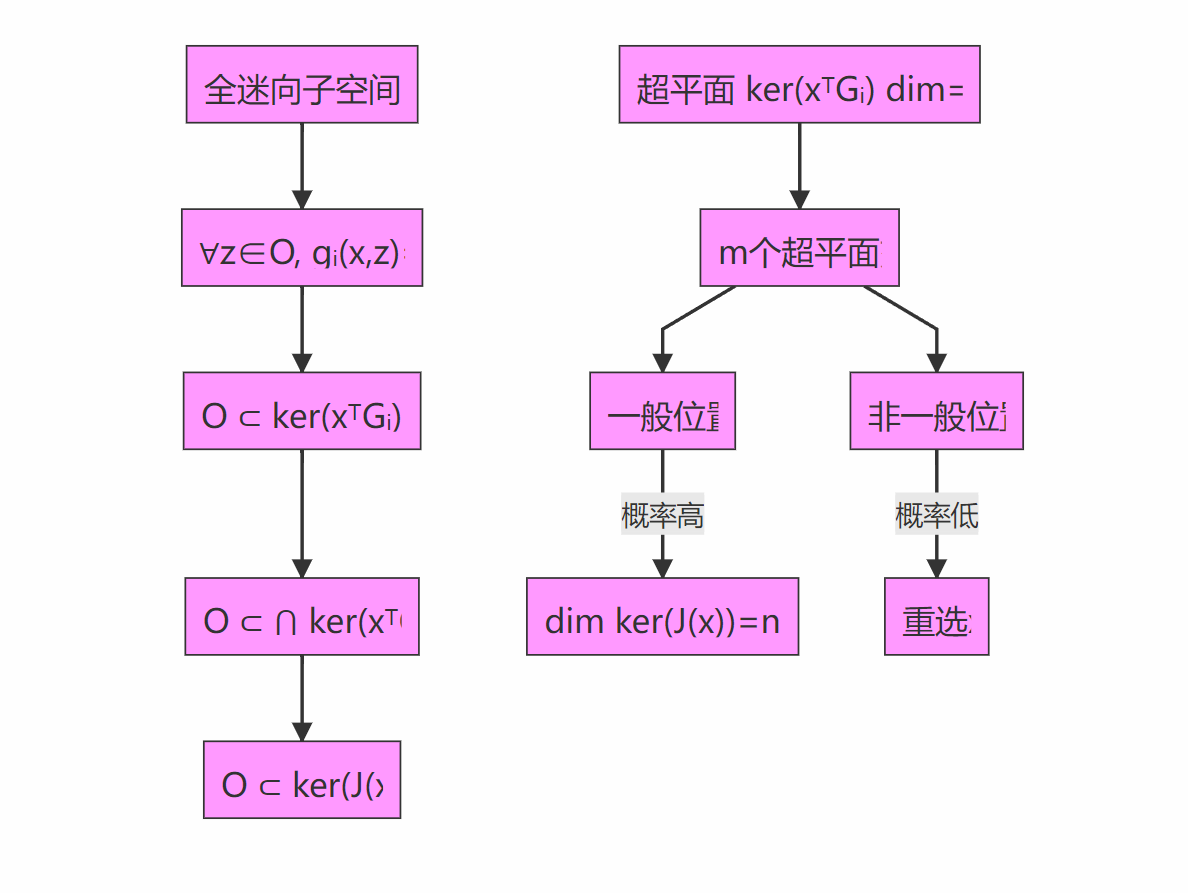
步骤 2：证明 $\dim \ker(J(\boldsymbol{x})) = n - m$ (一般情况)

1. 分析单个核

   • 每个 $G_i$ 秩为 $n$ 且 $\boldsymbol{x} \neq \mathbf{0}$
   • 线性形式 $g_{\boldsymbol{x}}^i = \boldsymbol{x}^T G_i$ 非零
   • 故每个 $\ker(\boldsymbol{x}^T G_i)$ 是 $\mathbb{F}_q^n$ 中的超平面（维数 $n-1$）

2. 超平面交点维数
   $\ker(J(\boldsymbol{x}))$ 是 $m$ 个超平面的交集：

   $$ \dim \left( \bigcap_{i=1}^m H_i \right) = n - m \quad \text{(当超平面处于一般位置)} $$

   其中 $H_i = \ker(\boldsymbol{x}^T G_i)$。

3. 处理非一般位置
   若超平面线性相关（如法向量线性相关），则：

   $$ \dim \ker(J(\boldsymbol{x})) > n - m $$

   但由 Schwartz-Zippel 引理：

   $$ \Pr_{}{(\boldsymbol{x})}\left[\text{超平面非一般位置}\right] \leq \frac{c}{q} $$

   ($c$ 为常数，$q$ 为域大小)

4. 随机化策略
   若遇非一般位置：

   • 重新随机选择 $\boldsymbol{x} \in \mathcal{O} \setminus {\mathbf{0}}$
   • 期望尝试次数为常数（因失败概率有界）

---

备注：雅可比矩阵解释

雅克比矩阵原始定义：

$$ \mathbf{J}_{\mathbf{f}} = \left[ \frac{\partial \mathbf{f}}{\partial x_1} \quad \cdots \quad \frac{\partial \mathbf{f}}{\partial x_n} \right] = \begin{bmatrix} \nabla^{\mathsf{T}} f_1 \\\\ \vdots \\\\ \nabla^{\mathsf{T}} f_m \end{bmatrix} = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\\\ \vdots & \ddots & \vdots \\\\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix} $$

$f$ 为二次型映射时：

$$ \mathbf{J}_{\mathbf{f}} = 2\mathbf{x}^TA $$

二次型映射的 Jacobi 矩阵推导

二次型映射的定义

设一个二次型映射 $f: \mathbb{R}^n \to \mathbb{R}$ 定义为：

$$ f(\mathbf{x}) = \mathbf{x}^{\mathsf{T}} A \mathbf{x} $$

其中：

$\mathbf{x} = [x_1, x_2, \ldots, x_n]^{\mathsf{T}}$ 是一个 $n \times 1$ 的列向量。$A$ 是一个 $n \times n$ 的实对称矩阵，即 $A = A^{\mathsf{T}}$。我们可以将 $A$ 的元素表示为 $a_{ij}$，对于 $i,j = 1, \ldots, n$。

展开二次型

将二次型 $f(\mathbf{x})$ 展开为求和形式：

$$ f(\mathbf{x}) = \sum_{i=1}^{n} \sum_{j=1}^{n} a_{ij} x_i x_j $$

计算偏导数

为了得到 Jacobi 矩阵（对于标量值函数，Jacobi 矩阵即为梯度向量的转置），我们需要计算 $f(\mathbf{x})$ 对每个 $x_k$ ($k=1, \ldots, n$) 的偏导数。

考虑对 $x_k$ 的偏导数：

$$ \frac{\partial f}{\partial x_k} = \frac{\partial}{\partial x_k} \left( \sum_{i=1}^{n} \sum_{j=1}^{n} a_{ij} x_i x_j \right) $$

在求和中，只有当 $i=k$ 或 $j=k$ 时，项 $a_{ij} x_i x_j$ 才包含 $x_k$。我们可以将求和项分为三类：

• $i=k, j \neq k$ 的项：$a_{kj} x_k x_j$
• $j=k, i \neq k$ 的项：$a_{ik} x_i x_k$
• $i=k, j=k$ 的项：$a_{kk} x_k x_k = a_{kk} x_k^2$

因此，偏导数可以写为：

$$ \begin{align*} \frac{\partial f}{\partial x_k} &= \sum_{j=1, j \neq k}^{n} \frac{\partial}{\partial x_k} (a_{kj} x_k x_j) + \sum_{i=1, i \neq k}^{n} \frac{\partial}{\partial x_k} (a_{ik} x_i x_k) + \frac{\partial}{\partial x_k} (a_{kk} x_k^2) \\ &= \sum_{j=1, j \neq k}^{n} a_{kj} x_j + \sum_{i=1, i \neq k}^{n} a_{ik} x_i + 2 a_{kk} x_k \end{align*} $$

由于矩阵 $A$ 是对称的，我们有 $a_{ik} = a_{ki}$。因此，第二个求和项可以改写为：

$$ \sum_{i=1, i \neq k}^{n} a_{ik} x_i = \sum_{i=1, i \neq k}^{n} a_{ki} x_i $$

现在，结合各项：

$$ \frac{\partial f}{\partial x_k} = \sum_{j=1, j \neq k}^{n} a_{kj} x_j + \sum_{i=1, i \neq k}^{n} a_{ki} x_i + 2 a_{kk} x_k $$

我们可以将这两个求和项重新整合，使其包含 $x_k$ 项。注意到 $\sum_{j=1}^{n} a_{kj} x_j$ 包含了 $a_{kk}x_k$，而 $\sum_{i=1}^{n} a_{ki} x_i$ 也包含了 $a_{kk}x_k$。因此，我们可以将原式改写为：

$$ \begin{align*} \frac{\partial f}{\partial x_k} &= \left( \sum_{j=1}^{n} a_{kj} x_j - a_{kk} x_k \right) + \left( \sum_{i=1}^{n} a_{ki} x_i - a_{kk} x_k \right) + 2 a_{kk} x_k \\ &= \sum_{j=1}^{n} a_{kj} x_j + \sum_{i=1}^{n} a_{ki} x_i \end{align*} $$

由于 $A$ 是对称矩阵，即 $a_{ki} = a_{ik}$，我们可以将第二个求和项的哑变量 $i$ 替换为 $j$，得到：

$$ \frac{\partial f}{\partial x_k} = \sum_{j=1}^{n} a_{kj} x_j + \sum_{j=1}^{n} a_{kj} x_j = \sum_{j=1}^{n} (a_{kj} + a_{jk}) x_j $$

由于 $A$ 是对称的， $a_{kj} = a_{jk}$，所以 $a_{kj} + a_{jk} = 2 a_{kj}$。

$$ \frac{\partial f}{\partial x_k} = \sum_{j=1}^{n} 2 a_{kj} x_j $$

构造 Jacobi 矩阵

Jacobi 矩阵 $\mathbf{J}_f$ 是一个 $1 \times n$ 的行向量（因为 $f$ 是从 $\mathbb{R}^n$ 到 $\mathbb{R}$ 的映射）：

$$ \mathbf{J}_f = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} & \cdots & \frac{\partial f}{\partial x_n} \end{bmatrix} $$

代入偏导数表达式：

$$ \mathbf{J_f} = \begin{bmatrix} \sum_{j=1}^{n} 2 a_{1j} x_j & \sum_{j=1}^{n} 2 a_{2j} x_j & \cdots & \sum_{j=1}^{n} 2 a_{nj} x_j \end{bmatrix} $$

这个矩阵可以写成矩阵乘法的形式：

$$ \mathbf{J_f} = 2 \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\\\ a_{21} & a_{22} & \cdots & a_{2n} \\\\ \vdots & \vdots & \ddots & \vdots \\\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} $$

即：

$$ \mathbf{J}_f = 2 \mathbf{x}^{\mathsf{T}} A $$

结论

综上所述，对于二次型映射 $f(\mathbf{x}) = \mathbf{x}^{\mathsf{T}} A \mathbf{x}$（其中 $A$ 是对称矩阵），其 Jacobi 矩阵为：

$$ \mathbf{J}_f = 2 \mathbf{x}^{\mathsf{T}} A $$

当域特征 $\neq 2$ 时（在 $F_q$ 中存在$2^{-1}$）：

$$ 2J(\boldsymbol{x}) = \mathbf{J}_G(\boldsymbol{x}) $$

其中 $\mathbf{J}_G$ 是 $G$ 的雅可比矩阵。此时：

$$ \ker(J(\boldsymbol{x})) = \ker(\mathbf{J}_G(\boldsymbol{x})) $$

这也解释了记法 “$J$” 的由来。

证明总结

Distinguisher

Summary

From One Vector to Rule By the properties of an istropic subspace and Jacobi Matrix, equivalent to forgery.

:)

Refferences

• Characteristics
• One Vector to Rule Them All
• Another Paper To Read