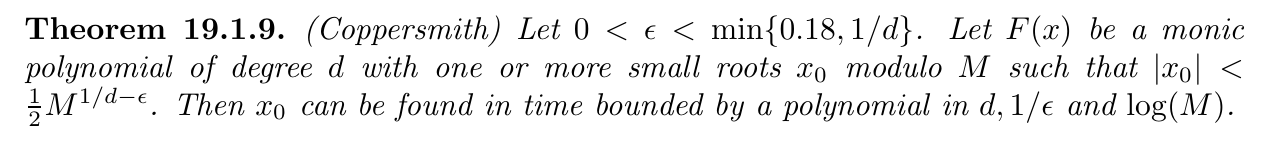RE:从零开始的crypto生活
模多项式求根问题
被认为计算困难的方程:
$$
p(x)=0\left(\operatorname{mod}N\right);
$$
在Zmod(N)的环下求解整数根。
$$
p(x,y)=0 \pmod{N}
$$
对于多变量多项式在Zmod(N)的环下求解一组整数根。
Coppersmith’s Method
概述

针对这样的思路,可以在格规约、移位多项式和求解common root等几个过程做优化,从而达到提升bound、加快规约速度等目的。Sagemath 中集成了这一方式,但我们也可以手动修改其中过程,以满足需要。
一般的Howgrave-Graham给出:

即,当给定一个上界 $X = N$ ,如果一个根 $x_0 \lt X$ ,那么我们当该多项式在整数环上时,$f(x_0)=0$ 依然成立。
这一引理通常被记为 Howgrave-Graham[22], 或 Hastad[19]

涉及范数证明的命题,时常会让我们想起柯西不等式,进而导出$l_1$范数和$l_2$范数间的关系。
为了更好理解,证明命题的功课时常不能忽略。
$l_1$ 和 $l_2$ 范数之间的关系
(编写公式,为了方便没有切换输入法)
Norm Relationships and Cauchy-Schwarz Inequality
For a vector $a=(a_1,\dots,a_n)$,then $l_1$-norm and the $l_2$-norm are defined as:
$$\Vert \mathbf{a}\Vert_1 =\sum_{i=1}^{i} |a_i| \quad\mathrm{and}\quad \Vert\mathbf{a}\Vert_2=\left(\sum_{i=1}^{n}|a_{i}|^2\right)^{1/2}.$$
The $l_1$-norm is generally larger than the $l_2$-norm, and they are related by:
$$\|\mathbf{a}\|_1\leq\sqrt{n}\|\mathbf{a}\|_2.$$
This relationship can be derived from the Cauchy-Schwarz inequality.
Cauchy-Schwarz Inequality:
The Cauchy-Schwarz inequality states that for any vectors a and b in $\mathbb{R}^n:$
$$
\left(\sum_{i=1}^na_ib_i\right)^2\leq\left(\sum_{i=1}^na_i^2\right)\left(\sum_{i=1}^nb_i^2\right).
$$
If we take b to be a vector of ones, $\mathbf{b}=(1,1,\ldots,1)$,we get:
$$
\left(\sum_{i=1}^na_i\right)^2\leq n\left(\sum_{i=1}^na_i^2\right).
$$
Taking the square root of both sides gives us the desired relationship:
$$
\sum_{i=1}^n|a_i|\leq\sqrt{n}\left(\sum_{i=1}^n|a_i|^2\right)^{1/2}.
$$
Applying This to the Problem
In the howgrave’s case,we are dealing with a polynomial $g(x)=\sum c_ix^i.$ The key steps in the inequality chain are:
Bounding the Polynomial’s Value:
$$
|g(x_0)|=\left|\sum_ic_ix_0^i\right|\leq\sum_i|c_ix_0^i|.
$$
Introducing a Bound on $x_0$:
$$
\sum_i|c_ix_0^i|\leq\sum_i|c_i|X^i
$$
where $x_0 \le X$.
$$
\sum_i|c_i|X^i = \sum_i|c_iX^i| \le\sqrt{n} \left(\sum_i |c_i X^i| \right )^{1/2}= \sqrt{n} \| g(xX)\| \lt N^m
$$
Here,$g(xX)=\sum c_i (xX)^i$.
与 Lattice 的关系
在前面我们完成了两个条件的初步解释:
Property 2 表明
$$
|g(x_0)| \lt N^m
$$
结合 Property 1 , 不难得出 $g(x_0)=0$ 的结论。
在此基础上,选定整数 $m \in \mathbb{Z}$ ,可以注意到存在这样的线性组合:
$$
h_{i,j}=x^jN^if^{m-i}(x).
$$
所得的 $h_{i,j}$ 均满足 $h_{i,j}(x_0)=0 \mod N^m$.
Lattice 出现:
用系数向量 $h_i$ 唯一标识 $h_{i,j}(x)$ 。
Regev 讲义的 intro 部分在定义 lattice 时,将其写为一种线性组合:

而在此处,$h_{i,j}$ 的线性组合也可构成 Lattice.
$$\mathcal{L} (h_{0},\dots,h_i) = \set{\sum x_i h_i\mid x\in\mathbb{Z}}$$
更为重要的是,在注意到我们定义的格$\mathcal{L}$中,短向量与系数均相对较小的多项式 $g(x)$ 一一对应,那么考虑到 Howgrave-Graham[22] 的形式,从直觉上可以考虑在短向量上应用这一引理,从而得到一个满足条件的小根 $x_0$:
$$
g(x_0)=0\mathrm{~mod~}N^m\mathrm{~and~}|g(x_0)|
在满足这一条件时,直接当做普通多项式处理求根即可。
再进一步,由于我们在构造 Lattice $\mathcal{L}$ 时, 给出先决条件, 所有的多项式 $h_{i,j}$ 共有一个根 $x_0$ .实际上,至此,我们完成了在 $(1)$ 的条件下的模多项式求根问题的一种求解方式。
实际上这依然是从根与多项式关系出发,化归到特定条件下的 SVP ,接下来我们处理 SVP 。
LLL 算法

回顾闵可夫斯基界下,任意 Lattice 均含有一个非零短向量$v’ \le \sqrt{n}\det(L)^{1/n}$.
对比两个不等式
$$
\begin{align} \|\mathbf{v}\| &\leq2^{\frac{n-1}4}\det(\mathcal{L})^{\frac1n} \\\\ \|v' \| &\le \sqrt{n}\det(\mathcal{L})^{\frac1n} \end{align}
$$
在此前定义的格 $\mathcal{L}$ 中,我们稍作分析
$$
\det (\mathcal{L})=N^{\Theta(m)},m \approx \log N.
$$
所以当两不等式右侧的 $\det(\mathcal{L})$ 足够大时,可以把 LLL 所得 output $v$ 视作可用的一个短向量。
可以看到误差在 Coppersmith 的语境下是可以接受的范围,而且天然的赋予了所得近似短向量 $v$ 一个上界限,进而我们考虑 H-G[22]

$$
\det(\mathcal{L})<\frac{N^{mn}}{n^{n/2}\cdot2^{\frac{(n-1)n}4}}\lt N^{mn}
$$
Enabling Condition
$$
\det(\mathcal{L}) \le N^{mn}
$$这一条件可用于优化$X$.接下来要详细的考虑如何构建这个Lattice $\mathcal{L}$
Speaking Mathematically

首先关注如何构造 $h_{i,j}(x)$ :
选取 $m \approx \frac{\log N}{\delta} $
$$
h_{i,j}(x)=x^jN^if(x)^{m-i}\mathrm{~for~}0\leq i
形成了一张 $n = m\delta \approx \log N$ 维 Lattice.
$$
\begin{cases} \det(L)&=\det(B)\approx N^{\frac{\delta m^2}2}X^{\frac{n^2}2} \\\\ n &= m\delta \\\\ N^{\frac{\delta m^2}2}X^{\frac{n^2}2} &\leq N^{mn}. \end{cases}
$$
可得
$$
X \le N^{1/\delta}
$$
分析到这里,我们已经初步得到可行的方案, 但尚未引入 $\beta$ 来优化 $X$ 的 bound.
算法的时间复杂度分析,本文略去。
上述做法的 Code 体现:
1
2
|
delta = f.degree()
g = [x**j * N**(m-i) * f**i for i in srange(m) for j in srange(delta)]
|
For $\beta,c,\epsilon$
我们在 sagemath 常用的 smal_root 方法, 通常有 $X,\beta,\epsilon$ 三个参数,和我们上面讨论的并不一致,本节继续探索这个问题。
$c$
$c$ 的引入是为了提高 $X$ 的上界。
这里直接考虑对 $N$ 处理

对于区间 $[-cN^{1/\delta},cN^{1/\delta}]$ ,直接考虑分为 $c$ 个大小为 $2N^{1/\delta}$ 的子区间,这样的子区间符合前文讨论的初等情况,那么运行 $c$ 次,便可以找出这个较大区间内的所有符合条件的根。
$\beta$
指数变换:

直接应用 $N$ 的一个较小因子而非 $N$ 本身,可以在时间复杂度上
$\epsilon$
一类特殊情况下的分析,引入了 $\epsilon$ .
由于更换了参考文献,符号有所更改.
$M = N,d= \delta$
其他保持一致即可。

不难发现, $\frac{1}{2}N^{\frac{1}{d}-\epsilon}$ 相对于 $cN^{\frac{\beta^2}{\delta}}$ 的形式,这里给出了 $c=\frac{1}{2},\beta = 1$, 又在 $\beta$ 其后增加了 $-\epsilon$ . 同时给定了限制:
$$
0 \lt \epsilon \lt \min\{0.18, 1/d\}
$$


证明到这里已经写明所引参数 $h$ 同待证明命题参数 $\epsilon$ , 而此时可以考虑应用条件 $X \lt \frac{1}{2}M^{1/d -\epsilon}$ .

进一步的,在实际参数中引入了 $m,t$ 来控制移位多项式,来构建 $\mathcal{L}$ .
具体可参见所附代码.
Open problem

至此,单变量的coppersmith求解小根问题的思考可以完美落幕。而格的优化亦或是求解公共根时的算法更改又是另一个新的问题了。
small_root in sage
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
|
def small_roots(self, X=None, beta=1.0, epsilon=None, **kwds):
"""
Let `N` be the characteristic of the base ring this polynomial
is defined over: ``N = self.base_ring().characteristic()``.
This method returns small roots of this polynomial modulo some
factor `b` of `N` with the constraint that `b >= N^\beta`.
Small in this context means that if `x` is a root of `f`
modulo `b` then `|x| < X`. This `X` is either provided by the
user or the maximum `X` is chosen such that this algorithm
terminates in polynomial time. If `X` is chosen automatically
it is `X = ceil(1/2 N^{\beta^2/\delta - \epsilon})`.
The algorithm may also return some roots which are larger than `X`.
'This algorithm' in this context means Coppersmith's algorithm for finding
small roots using the LLL algorithm. The implementation of this algorithm
follows Alexander May's PhD thesis referenced below.
INPUT:
- ``X`` -- an absolute bound for the root (default: see above)
- ``beta`` -- compute a root mod `b` where `b` is a factor of `N` and `b
\ge N^\beta`. (Default: 1.0, so `b = N`.)
- ``epsilon`` -- the parameter `\epsilon` described above. (Default: `\beta/8`)
- ``**kwds`` -- passed through to method :meth:`Matrix_integer_dense.LLL() <sage.matrix.matrix_integer_dense.Matrix_integer_dense.LLL>`.
EXAMPLES:
First consider a small example::
sage: N = 10001
sage: K = Zmod(10001)
sage: P.<x> = PolynomialRing(K, implementation='NTL')
sage: f = x^3 + 10*x^2 + 5000*x - 222
This polynomial has no roots without modular reduction (i.e. over `\ZZ`)::
sage: f.change_ring(ZZ).roots()
[]
To compute its roots we need to factor the modulus `N` and use the Chinese
remainder theorem::
sage: p,q = N.prime_divisors()
sage: f.change_ring(GF(p)).roots()
[(4, 1)]
sage: f.change_ring(GF(q)).roots()
[(4, 1)]
sage: crt(4, 4, p, q)
4
This root is quite small compared to `N`, so we can attempt to
recover it without factoring `N` using Coppersmith's small root
method::
sage: f.small_roots()
[4]
An application of this method is to consider RSA. We are using 512-bit RSA
with public exponent `e=3` to encrypt a 56-bit DES key. Because it would be
easy to attack this setting if no padding was used we pad the key `K` with
1s to get a large number::
sage: Nbits, Kbits = 512, 56
sage: e = 3
We choose two primes of size 256-bit each::
sage: p = 2^256 + 2^8 + 2^5 + 2^3 + 1
sage: q = 2^256 + 2^8 + 2^5 + 2^3 + 2^2 + 1
sage: N = p*q
sage: ZmodN = Zmod( N )
We choose a random key::
sage: K = ZZ.random_element(0, 2^Kbits)
and pad it with 512-56=456 1s::
sage: Kdigits = K.digits(2)
sage: M = [0]*Kbits + [1]*(Nbits-Kbits)
sage: for i in range(len(Kdigits)): M[i] = Kdigits[i]
sage: M = ZZ(M, 2)
Now we encrypt the resulting message::
sage: C = ZmodN(M)^e
To recover `K` we consider the following polynomial modulo `N`::
sage: P.<x> = PolynomialRing(ZmodN, implementation='NTL')
sage: f = (2^Nbits - 2^Kbits + x)^e - C
and recover its small roots::
sage: Kbar = f.small_roots()[0]
sage: K == Kbar
True
The same algorithm can be used to factor `N = pq` if partial
knowledge about `q` is available. This example is from the
Magma handbook:
First, we set up `p`, `q` and `N`::
sage: length = 512
sage: hidden = 110
sage: p = next_prime(2^int(round(length/2)))
sage: q = next_prime( round(pi.n()*p) )
sage: N = p*q
Now we disturb the low 110 bits of `q`::
sage: qbar = q + ZZ.random_element(0,2^hidden-1)
And try to recover `q` from it::
sage: F.<x> = PolynomialRing(Zmod(N), implementation='NTL')
sage: f = x - qbar
We know that the error is `\le 2^{\text{hidden}}-1` and that the modulus
we are looking for is `\ge \sqrt{N}`::
sage: from sage.misc.verbose import set_verbose
sage: set_verbose(2)
sage: d = f.small_roots(X=2^hidden-1, beta=0.5)[0] # time random
verbose 2 (<module>) m = 4
verbose 2 (<module>) t = 4
verbose 2 (<module>) X = 1298074214633706907132624082305023
verbose 1 (<module>) LLL of 8x8 matrix (algorithm fpLLL:wrapper)
verbose 1 (<module>) LLL finished (time = 0.006998)
sage: q == qbar - d
True
REFERENCES:
Don Coppersmith. *Finding a small root of a univariate modular equation.*
In Advances in Cryptology, EuroCrypt 1996, volume 1070 of Lecture
Notes in Computer Science, p. 155--165. Springer, 1996.
http://cr.yp.to/bib/2001/coppersmith.pdf
Alexander May. *New RSA Vulnerabilities Using Lattice Reduction Methods.*
PhD thesis, University of Paderborn, 2003.
http://www.cs.uni-paderborn.de/uploads/tx_sibibtex/bp.pdf
"""
from sage.misc.verbose import verbose
from sage.matrix.constructor import Matrix
from sage.rings.all import RR
N = self.parent().characteristic()
if not self.is_monic():
raise ArithmeticError("Polynomial must be monic.")
beta = RR(beta)
if beta <= 0.0 or beta > 1.0:
raise ValueError("0.0 < beta <= 1.0 not satisfied.")
f = self.change_ring(ZZ)
P,(x,) = f.parent().objgens()
delta = f.degree()
if epsilon is None:
epsilon = beta/8
verbose("epsilon = %d"%epsilon, level=2)
m = max(beta**2/(delta * epsilon), 7*beta/delta).ceil()
verbose("m = %d"%m, level=2)
t = int( ( delta*m*(1/beta -1) ).floor() )
verbose("t = %d"%t, level=2)
if X is None:
X = (0.5 * N**(beta**2/delta - epsilon)).ceil()
verbose("X = %s"%X, level=2)
# we could do this much faster, but this is a cheap step
# compared to LLL
g = [x**j * N**(m-i) * f**i for i in range(m) for j in range(delta) ]
g.extend([x**i * f**m for i in range(t)]) # h
B = Matrix(ZZ, len(g), delta*m + max(delta,t) )
for i in range(B.nrows()):
for j in range( g[i].degree()+1 ):
B[i,j] = g[i][j]*X**j
B = B.LLL(**kwds)
f = sum([ZZ(B[0,i]//X**i)*x**i for i in range(B.ncols())])
R = f.roots()
ZmodN = self.base_ring()
roots = set([ZmodN(r) for r,m in R if abs(r) <= X])
Nbeta = N**beta
return [root for root in roots if N.gcd(ZZ(self(root))) >= Nbeta]
|
应用 flatter 简单 coding 一下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
|
#sage10.3 Halois
# if ur running a brute force attack on a polynomial, this is not your weapon, Too many system calls can drain your time
DEBUG = False # set on True to see warnings
def flat_roots(f, bounds, m=1, d=None):
import itertools, subprocess
if DEBUG:
import warnings
warnings.filterwarnings('ignore')
def dump(M):
return "[{}]".format("\n".join("[{}]".format(" ".join(map(str, r))) for r in M))
def parse_row(r):
return map(ZZ, r.split())
def parse(x):
x = x.replace("\n", "")
assert x[0] == "["
assert x[-1] == "]"
return Matrix(ZZ, map(parse_row, x[2:-2].split("][")))
def flatter(M):
try:
PATH = FLATTER_PATH
except NameError:
print("Warning: using `flatter` if it can be found on $PATH. Set `FLATTER_PATH` to the command if this fails.") if DEBUG else None
PATH = "flatter"
try:
ARGS = FLATTER_ARGS
except:
ARGS = []
return parse(subprocess.check_output([PATH, *ARGS], input=dump(M).encode()).decode())
# Because univariate and multivariate are just different enough to make you crazy , but in sage10.3 we get a grace way
PR = PolynomialRing(f.parent(), 0, ()).flattening_morphism().codomain()
f = PR(f)
orig = f
if not d:
d = f.degree()
R = f.base_ring()
N = R.cardinality()
f /= f.coefficients().pop(0)
f = f.change_ring(ZZ)
G = Sequence([], f.parent())
for i in range(m+1):
base = N^(m-i) * f^i
for shifts in itertools.product(range(d), repeat=len(f.parent().gens())):
g = base * prod(map(power, f.parent().gens(), shifts))
G.append(g)
B, monomials = G.coefficient_matrix()
monomials = vector(monomials)
factors = [monomial(*bounds) for monomial in monomials]
for i, factor in enumerate(factors):
B.rescale_col(i, factor)
B = flatter(B.dense_matrix())
B = B.change_ring(QQ)
for i, factor in enumerate(factors):
B.rescale_col(i, 1/factor)
H = Sequence([], f.parent().change_ring(QQ))
roots = []
for h in filter(None, B*monomials):
H.append(h)
I = H.ideal()
if I.dimension() == -1:
H.pop()
elif I.dimension() == 0:
roots = []
for root in I.variety(ring=ZZ):
root = tuple(R(root[var]) for var in f.parent().gens())
if gcd(ZZ(orig(*root)), N) != 1:
roots.append(root)
return roots
return roots
def install_flatter():
import os
if not os.path.exists("flatter/bin/flatter"):
os.system("rm -rf flatter \
&& git clone https://github.com/keeganryan/flatter \
&& cd flatter && sed -i 's/SHARED/STATIC/g' src/CMakeLists.txt \
&& mkdir build \
&& cd build \
&& cmake .. \
-DCMAKE_BUILD_TYPE=Release \
-DCMAKE_INSTALL_PREFIX=..\
-DCMAKE_CXX_FLAGS='-march=native' \
&& make install")
global FLATTER_PATH
FLATTER_PATH = os.path.join(os.getcwd(), "flatter", "bin", "flatter")
|
Reference